1 ArtiSynth Overview 1.1 System structure 1.3 Basic packages

1.2 Physics simulation

Only a brief summary of ArtiSynth physics simulation is described here. Full details are given in [11] and in the related overview paper.

For purposes of physics simulation, the components of a MechModel are grouped as follows:

Dynamic components: Components, such as a particles and rigid bodies, that contain position and velocity state, as well as mass. All dynamic components are instances of the Java interface DynamicComponent.
Force effectors: Components, such as springs or finite elements, that exert forces between dynamic components. All force effectors are instances of the Java interface ForceEffector.
Constrainers: Components that enforce constraints between dynamic components. All constrainers are instances of the Java interface Constrainer.
Attachments: Attachments between dynamic components. While technically these are constraints, they are implemented using a different approach. All attachment components are instances of DynamicAttachment.

The positions, velocities, and forces associated with all the dynamic components are denoted by the composite vectors ${\bf q}$ , ${\bf u}$ , and ${\bf f}$ . In addition, the composite mass matrix is given by ${\bf M}$ . Newton’s second law then gives

${\bf f}=\frac{d{\bf M}{\bf u}}{dt}={\bf M}\dot{\bf u}+\dot{\bf M}{\bf u},$

(1.1)

where the $\dot{\bf M}{\bf u}$ accounts for various “fictitious” forces.

Each integration step involves solving for the velocities ${\bf u}^{k+1}$ at time step given the velocities and forces at step . One way to do this is to solve the expression

${\bf M}\,{\bf u}^{k+1}={\bf M}{\bf u}^{k}+h\bar{\bf f}$

(1.2)

for ${\bf u}^{k+1}$ , where is the step size and $\bar{\bf f}\equiv{\bf f}-\dot{\bf M}{\bf u}$ . Given the updated velocities ${\bf u}^{k+1}$ , one can determine $\dot{\bf q}^{k+1}$ from

$\dot{\bf q}^{k+1}={\bf Q}{\bf u}^{k+1},$

(1.3)

where ${\bf Q}$ accounts for situations (like rigid bodies) where $\dot{\bf q}\neq{\bf u}$ , and then solve for the updated positions using

${\bf q}^{k+1}={\bf q}^{k}+h\dot{\bf q}^{k+1}.$

(1.4)

(1.2) and (1.4) together comprise a simple symplectic Euler integrator.

In addition to forces, bilateral and unilateral constraints give rise to locally linear constraints on ${\bf u}$ of the form

${\bf G}({\bf q}){\bf u}=0,\qquad{\bf N}({\bf q}){\bf u}\geq 0.$

(1.5)

Bilateral constraints may include rigid body joints, FEM incompressibility, and point-surface constraints, while unilateral constraints include contact and joint limits. Constraints give rise to constraint forces (in the directions ${\bf G}({\bf q})^{T}$ and ${\bf N}({\bf q})^{T}$ ) which supplement the forces of (1.1) in order to enforce the constraint conditions. In addition, for unilateral constraints, we have a complementarity condition in which ${\bf N}{\bf u}>0$ implies no constraint force, and a constraint force implies ${\bf N}{\bf u}=0$ . Any given constraint usually involves only a few dynamic components and so ${\bf G}$ and ${\bf N}$ are generally sparse.

Adding constraints to the velocity solve (1.2) leads to a mixed linear complementarity problem (MLCP) of the form

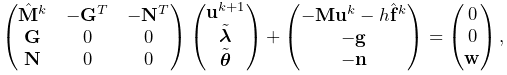	$\displaystyle\left(\begin{matrix}\hat{\bf M}^{k}&-{\bf G}^{T}&-{\bf N}^{T}\\ {\bf G}&0&0\\ {\bf N}&0&0\end{matrix}\right)\left(\begin{matrix}{\bf u}^{k+1}\\ \tilde{\boldsymbol{\lambda}}\\ \tilde{\boldsymbol{\theta}}\end{matrix}\right)+\left(\begin{matrix}-{\bf M}{% \bf u}^{k}-h\hat{\bf f}^{k}\\ -{\bf g}\\ -{\bf n}\end{matrix}\right)=\left(\begin{matrix}0\\ 0\\ {\bf w}\end{matrix}\right),$
	$\displaystyle 0\leq\boldsymbol{\theta}\perp{\bf w}\geq 0,$		(1.6)

where ${\bf w}$ is a slack variable, $\tilde{\boldsymbol{\lambda}}$ and $\tilde{\boldsymbol{\theta}}$ give the force constraint impulses over the time step, and ${\bf g}$ and ${\bf n}$ are derivative terms defined by

${\bf g}\equiv-h\dot{\bf G}{\bf u}^{k},\quad{\bf n}\equiv-h\dot{\bf N}{\bf u}^{% k},$

(1.7)

to account for time variations in ${\bf G}$ and ${\bf N}$ . In addition, $\hat{\bf M}$ and $\hat{\bf f}$ are ${\bf M}$ and $\bar{\bf f}$ augmented with stiffness and damping terms terms to accommodate implicit integration, which is often required for problems involving deformable bodies. The actual constraint forces $\boldsymbol{\lambda}$ and $\boldsymbol{\theta}$ can be determined by dividing the impulses by the time step :

$\boldsymbol{\lambda}=\tilde{\boldsymbol{\lambda}}/h,\quad\boldsymbol{\theta}=% \tilde{\boldsymbol{\theta}}/h.$

(1.8)

We note here that ArtiSynth uses a full coordinate formulation, in which the position of each dynamic body is solved using full, or unconstrained, coordinates, with constraint relationships acting to restrict these coordinates. In contrast, some other simulation systems, including OpenSim [7], use reduced coordinates, in which the system dynamics are formulated using a smaller set of coordinates (such as joint angles) that implicitly take the system’s constraints into account. Each methodology has its own advantages. Reduced formulations yield systems with fewer degrees of freedom and no constraint errors. On the other hand, full coordinates make it easier to combine and connect a wide range of components, including rigid bodies and FEM models.

Attachments between components can be implemented by constraining the velocities of the attached components using special constraints of the form

${\bf u}_{j}=-{\bf G}_{j\alpha}{\bf u}_{\alpha}$

(1.9)

where ${\bf u}_{j}$ and ${\bf u}_{\alpha}$ denote the velocities of the attached and non-attached components. The constraint matrix ${\bf G}_{j\alpha}$ is sparse, with a non-zero block entry for each master component to which the attached component is connected. The simplest case involves attaching a point to another point , with the simple velocity relationship

${\bf u}_{j}={\bf u}_{k}$

(1.10)

That means that ${\bf G}_{j\alpha}$ has a single entry of $-{\bf I}$ (where ${\bf I}$ is the $3\times 3$ identity matrix) in the -th block column. Another common case involves connecting a point to a rigid frame . The velocity relationship for this is

${\bf u}_{j}={\bf u}_{k}-{\bf l}_{j}\times\boldsymbol{\omega}_{k}$

(1.11)

where ${\bf u}_{k}$ and $\boldsymbol{\omega}_{k}$ are the translational and rotational velocity of the frame and $l_{j}$ is the location of the point relative to the frame’s origin (as seen in world coordinates). The corresponding ${\bf G}_{j\alpha}$ contains a single $3\times 6$ block entry of the form

$\left(\begin{matrix}{\bf I}&[l_{j}]\end{matrix}\right)$

(1.12)

in the block column, where

$[l]\equiv\left(\begin{matrix}0&-l_{z}&l_{y}\\ l_{z}&0&-l_{x}\\ -l_{y}&l_{x}&0\end{matrix}\right)$

(1.13)

is a skew-symmetric cross product matrix. The attachment constraints ${\bf G}_{j\alpha}$ could be added directly to (1.6), but their special form allows us to explicitly solve for ${\bf u}_{j}$ , and hence reduce the size of (1.6), by factoring out the attached velocities before solution.

The MLCP (1.6) corresponds to a single step integrator. However, higher order integrators, such as Newmark methods, usually give rise to MLCPs with an equivalent form. Most ArtiSynth integrators use some variation of (1.6) to determine the system velocity at each time step.

To set up (1.6), the MechModel component hierarchy is traversed and the methods of the different component types are queried for the required values. Dynamic components (type DynamicComponent) provide ${\bf q}$ , ${\bf u}$ , and ${\bf M}$ ; force effectors (ForceEffector) determine $\hat{\bf f}$ and the stiffness/damping augmentation used to produce $\hat{\bf M}$ ; constrainers (Constrainer) supply ${\bf G}$ , ${\bf N}$ , ${\bf g}$ and ${\bf n}$ , and attachments (DynamicAttachment) provide the information needed to factor out attached velocities.

1.1 System structure Bibliography 1.3 Basic packages

Generated on Wed Jul 24 21:23:12 2024 by LaTeXML [LOGO]