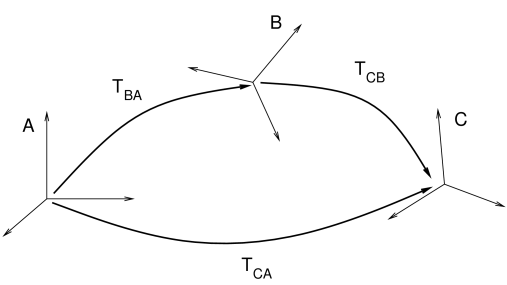
A.2 Rigid transforms
Rigid transforms are used to specify both the transformation of points and vectors between coordinate frames, as well as the relative position and orientation between coordinate frames.
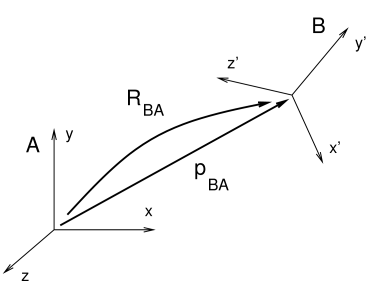
Consider two 3D coordinate frames in space, A and B (Figure
A.3). The translational position of B with respect to A
can be described by a vector ![]() from the origin of A to the
origin of B (described with respect to frame A). Meanwhile, the
orientation of B with respect to A can be described by the
from the origin of A to the
origin of B (described with respect to frame A). Meanwhile, the
orientation of B with respect to A can be described by the ![]() rotation matrix
rotation matrix ![]() (Section A.1). The
combined position and orientation of B with respect to A is known as
the pose of B with respect to A.
(Section A.1). The
combined position and orientation of B with respect to A is known as
the pose of B with respect to A.
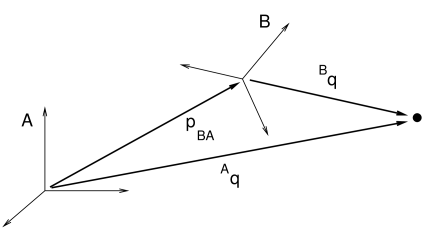
Now, assume we have a 3D point ![]() , and consider its coordinates with
respect to both frames A and B (Figure A.4). Given the
pose descriptions given above, it is fairly straightforward to show
that
, and consider its coordinates with
respect to both frames A and B (Figure A.4). Given the
pose descriptions given above, it is fairly straightforward to show
that
| (A.10) |
and, given (A.2), that
| (A.11) |
If we extend our points into a 4D homogeneous coordinate space
with the fourth coordinate ![]() equal to 1, i.e.,
equal to 1, i.e.,
| (A.12) |
then (A.10) and (A.11) can be simplified to
where
| (A.13) |
and
| (A.14) |
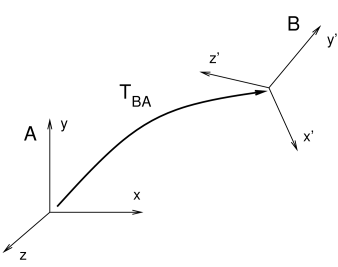
![]() is the
is the ![]() rigid transform matrix that
transforms points from B to A and also describes the pose of
B with respect to A (Figure A.5).
rigid transform matrix that
transforms points from B to A and also describes the pose of
B with respect to A (Figure A.5).
It is straightforward to show that ![]() and
and ![]() describe the orientation and position of
describe the orientation and position of ![]() with respect to
with respect to
![]() , and so therefore
, and so therefore
| (A.15) |
Note that if we are transforming a vector ![]() instead of a point
between B and A, then we are only concerned about relative orientation
and the vector transforms (A.3) and
(A.4) should be used instead.
However, we can express these using
instead of a point
between B and A, then we are only concerned about relative orientation
and the vector transforms (A.3) and
(A.4) should be used instead.
However, we can express these using ![]() if
we embed vectors in a homogeneous coordinate space
with the fourth coordinate
if
we embed vectors in a homogeneous coordinate space
with the fourth coordinate ![]() equal to 0, i.e.,
equal to 0, i.e.,
| (A.16) |
so that