A Mathematical Review A.4 Rotational velocity A.6 Spatial inertia

A.5 Spatial velocities and forces

Given two 3D coordinate frames A and B, the spatial velocity, or twist, $\hat{\bf v}_{BA}$ of B with respect to A is given by the 6D composition of the translational velocity ${\bf v}_{BA}$ of the origin of B with respect to A and the angular velocity $\boldsymbol{\omega}_{BA}$ :

$\hat{\bf v}_{BA}\equiv\left(\begin{matrix}{\bf v}_{BA}\\ \boldsymbol{\omega}_{BA}\end{matrix}\right).$

(A.24)

Similarly, the spatial force, or wrench, $\hat{\bf f}$ acting on a frame B is given by the 6D composition of the translational force ${\bf f}_{B}$ acting on the frame’s origin and the moment $\boldsymbol{\tau}$ , or torque, acting through the frame’s origin:

$\hat{\bf f}_{B}\equiv\left(\begin{matrix}{\bf f}_{B}\\ \boldsymbol{\tau}_{B}\end{matrix}\right).$

(A.25)

Figure A.9: Two frames A and B rigidly connected within a rigid body and moving with respect to a third frame C.

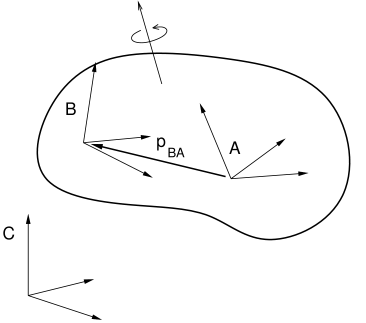
If we have two frames and rigidly connected within a rigid body (Figure A.9), and we know the spatial velocity $\hat{\bf v}_{BC}$ of with respect to some third frame , we may wish to know the spatial velocity $\hat{\bf v}_{AC}$ of with respect to . The angular velocity components are the same, but the translational velocity components are coupled by the angular velocity and the offset ${\bf p}_{BA}$ between and , so that

${\bf v}_{AC}={\bf v}_{BC}+{\bf p}_{BA}\times\boldsymbol{\omega}_{BC}.$

$\hat{\bf v}_{AC}$ is hence related to $\hat{\bf v}_{BC}$ via

$\left(\begin{matrix}{\bf v}_{AC}\\ \boldsymbol{\omega}_{AC}\end{matrix}\right)=\left(\begin{matrix}{\bf I}&[{\bf p% }_{BA}]\\ 0&{\bf I}\end{matrix}\right)\,\left(\begin{matrix}{\bf v}_{BC}\\ \boldsymbol{\omega}_{BC}\end{matrix}\right).$

where $[{\bf p}_{BA}]$ is defined by (A.22).

The above equation assumes that all quantities are expressed with respect to the same coordinate frame. If we instead consider $\hat{\bf v}_{AC}$ and $\hat{\bf v}_{BC}$ to be represented in frames and , respectively, then we can show that

${}^{A}\hat{\bf v}_{AC}={\bf X}_{BA}\,{}^{B}\hat{\bf v}_{BC},$

(A.26)

where

${\bf X}_{BA}\equiv\left(\begin{matrix}{\bf R}_{BA}&[{\bf p}_{BA}]{\bf R}_{BA}% \\ 0&{\bf R}_{BA}\end{matrix}\right).$

(A.27)

The transform ${\bf X}_{BA}$ is easily formed from the components of the rigid transform ${\bf T}_{BA}$ relating to .

The spatial forces $\hat{\bf f}_{A}$ and $\hat{\bf f}_{B}$ acting on frames and within a rigid body are related in a similar way, only with spatial forces, it is the moment that is coupled through the moment arm created by ${\bf p}_{BA}$ , so that

$\boldsymbol{\tau}_{A}=\boldsymbol{\tau}_{B}+{\bf p}_{BA}\times{\bf f}_{B}.$

If we again assume that $\hat{\bf f}_{A}$ and $\hat{\bf f}_{B}$ are expressed in frames and , we can show that

${}^{A}\hat{\bf f}_{A}={\bf X}^{*}_{BA}\,{}^{B}\hat{\bf f}_{B},$

(A.28)

where

${\bf X}^{*}_{BA}\equiv\left(\begin{matrix}{\bf R}_{BA}&0\\ ~{}[{\bf p}_{BA}]{\bf R}_{BA}&{\bf R}_{BA}\end{matrix}\right).$

(A.29)

A.4 Rotational velocity Bibliography A.6 Spatial inertia

Generated on Tue Aug 12 13:46:32 2025 by LaTeXML [LOGO]