6 Finite Element Models 6.6 Frame attachments 6.8 Varying and augmenting material behaviors

6.7 Incompressibility

FEM incompressibility within ArtiSynth is enforced by trying to ensure that the volume of an FEM remains locally constant. This, in turn, is accomplished by constraining nodal velocities so that the local volume change, or divergence, is zero (or close to zero). There are generally two ways to do this:

•

Hard incompressibility, which sets up explicit constraints on the nodal velocities;
•

Soft incompressibility, which uses a restoring pressure based on a potential field to try to keep the volume constant.

Both of these methods operate independently, and both can be used either separately or together. Generally speaking, hard incompressibility will result in incompressibility being more rigorously enforced, but at the cost of increased computation time and (sometimes) less stability. Soft incompressibility allows the application to control the restoring force used to enforce incompressibility, usually by adjusting the value of the bulk modulus material property. As the bulk modulus is increased, soft incompressibility starts to act more like ‘hard’ incompressibility, with an infinite bulk modulus corresponding to perfect incompressibility. However, very large bulk modulus values will generally produce stability problems.

Incompressibility is not currently implemented for shell elements. Applying hard incompressibility to a shell element will have no effect on its behavior. If soft incompressibility is applied, by supplying the element with an incompressible material, then only the deviatoric component of that material will have any effect; the dilational component will generate no stress.

6.7.1 Volume regions and locking

Both hard and soft incompressibility can be applied to different regions of local volume. From larger to smaller, these regions are:

•

Nodal - the local volume surrounding each node;
•

Element - the volume of each element;
•

Full - the volume at each integration point.

Element-based incompressibility is the standard method generally seen in the literature. However, it tends not to work well for tetrahedral meshes, because constraining the volume of each tet in a tetrahedral mesh tends to over constrain the system. This is because the number of tets in a large tetrahedral mesh is often , where is the number of nodes, and so putting a volume constraint on each element may result in constraints, which exceeds the degrees of freedom (DOF) in the FEM. This overconstraining results in an artificially increased stiffness known as locking. Because of locking, for tetrahedrally based meshes it may be better to use nodal-based incompressibility, which creates a single volume constraint around each node, resulting in only constraints, leaving DOF to handle the remaining deformation. However, nodal-based incompressibility is computationally more costly than element-based and may not be as stable.

Generally, the best solution for incompressible problems is to use element-based incompressibility with a mesh consisting of hexahedra, or primarily hexahedra and a mix of other elements (the latter commonly being known as a hex dominant mesh). For hex-based meshes, the number of elements is roughly equal to the number of nodes, and so adding a volume constraint for each element imposes constraints on the model, which (like nodal incompressibility) leaves DOF to handle the remaining deformation.

Full incompressibility tries to control the volume at each integration point within each element, which almost always results in a large number of volumetric constraints and hence locking. It is therefore not commonly used and is provided mostly for debugging and diagnostic purposes.

6.7.2 Hard incompressibility

Hard incompressibility is controlled by the incompressible property of the FEM, which can be set to one of the following values of the enumerated type FemModel.IncompMethod:

OFF: No hard incompressibility enforced.
ELEMENT: Element-based hard incompressibility enforced (Section 6.7.1).
NODAL: Nodal-based hard incompressibility enforced (Section 6.7.1).
AUTO: Selects either ELEMENT or NODAL, with the former selected if the number of elements is less than or equal to the number of nodes.
ON: Same as AUTO.

Hard incompressibility uses explicit constraints on the nodal velocities to enforce the incompressibility, which increases computational cost. Also, if the number of constraints is too large, perturbed pivot errors may be encountered by the solver. However, hard incompressibility can in principle handle situations where complete incompressibility is required. It is equivalent to the mixed u-P formulation used in commercial FEM codes (such as ANSYS), and the Lagrange multipliers computed for the constraints are pressure impulses.

Hard incompressibility can be applied in addition to soft incompressibility, in which case it will provide additional incompressibility enforcement on top of that provided by the latter. It can also be applied to linear materials, which are not themselves able to emulate true incompressible behavior (Section 6.7.4).

6.7.3 Soft incompressibility

Soft incompressibility enforces incompressibility using a restoring pressure that is controlled by a volume-based energy potential. It is only available for FEM materials that are subclasses of IncompressibleMaterial. The energy potential is a function of the determinant of the deformation gradient, and is scaled by the material’s bulk modulus $\kappa$ . The restoring pressure is given by

$p=\frac{\partial U}{\partial J}.$

(6.5)

Different potentials can be selected by setting the bulkPotential property of the incompressible material, whose value is an instance of IncompressibleMaterial.BulkPotential. Currently there are two different potentials:

QUADRATIC

The potential and associated pressure are given by

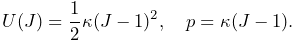
$U(J)=\frac{1}{2}\kappa(J-1)^{2},\quad p=\kappa(J-1).$

(6.6)

LOGARITHMIC

The potential and associated pressure are given by

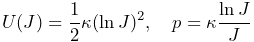
$U(J)=\frac{1}{2}\kappa(\ln J)^{2},\quad p=\kappa\frac{\ln J}{J}$

(6.7)

The default potential is QUADRATIC, which may provide slightly improved stability characteristics. However, we have not noticed significant differences between the two potentials in practice.

How soft incompressibility is applied within an FEM model is controlled by the FEM’s softIncompMethod property, which can be set to one of the following values of the enumerated type FemModel.IncompMethod:

ELEMENT: Element-based soft incompressibility enforced (Section 6.7.1).
NODAL: Nodal-based soft incompressibility enforced (Section 6.7.1).
AUTO: Selects either ELEMENT or NODAL, with the former selected if the number of elements is less than or equal to the number of nodes.
FULL: Incompressibility enforced at each integration point (Section 6.7.1).

6.7.4 Incompressibility and linear materials

Within a linear material, incompressibility is controlled by Poisson’s ratio $\nu$ , which for isotropic materials can assume a value in the range . This specifies the amount of transverse contraction (or expansion) exhibited by the material as it compressed or extended along a particular direction. A value of allows the material to be compressed or extended without any transverse contraction or expansion, while a value of in theory indicates a perfectly incompressible material. However, setting $\nu=0.5$ in practice causes a division by zero, so only values close to 0.5 (such as 0.49) can be used.

Moreover, the incompressibility only applies to small displacements, so that even with $\nu=0.49$ it is still possible to squash a linear FEM completely flat if enough force is applied. If true incompressible behavior is desired with a linear material, then one must also use hard incompressibility (Section 6.7.2).

6.7.5 Using incompressibility in practice

As mentioned above, when modeling incompressible models, we have found that the best practice is to use, if possible, either a hex or hex-dominant mesh, along with element-based incompressibility.

Hard incompressibility allows the handling of full incompressibility but at the expense of greater computational cost and often less stability. When modeling biomechanical materials, it is often permissible to use only soft incompressibility, partly since biomechanical materials are rarely completely incompressible. When implementing soft incompressibility, it is common practice to set the bulk modulus to something like 100 times the other (deviatoric) stiffnesses of the material.

We have found stability behavior to be complex, and while hard incompressibility often results in less stable behavior, this is not always the case: in some situations the stronger enforcement afforded by hard incompressibility actually improves stability.

6.6 Frame attachments Bibliography 6.8 Varying and augmenting material behaviors

Generated on Tue Mar 26 13:12:56 2024 by LaTeXML [LOGO]