6 Finite Element Models 6.9 Muscle activated FEM models 6.11 Stress, strain and strain energy

6.10 Material types

ArtiSynth FEM models support a variety of material types, including linear, hyperelastic, and activated muscle materials, described in the sections below. These can be used to supply the primary material for either an entire FEM model or for specific elements (using the setMaterial() methods for either). They can also be used to supply auxiliary materials, whose behavior is superimposed on the underlying material, via either material bundles (Section 6.8) or, for FemMuscleModels, muscle bundles (Section 6.9). Many of the properties for a given material can be bound to a scalar or vector field (Section 7.2) to allow their values to vary across an FEM model. In the descriptions below, properties for which this is true will have a $\checkmark$ indicated under the “Field” entry in the material’s property table.

All materials are defined in the package artisynth.core.materials.

6.10.1 Linear

Linear materials determine Cauchy stress $\boldsymbol{\sigma}$ as a linear mapping from the small deformation Cauchy strain $\boldsymbol{\epsilon}$ ,

$\boldsymbol{\sigma}=\mathcal{D}:\boldsymbol{\epsilon},$

(6.7)

where $\mathcal{D}$ is the elasticity tensor. Both the stress and strain are symmetric matrices,

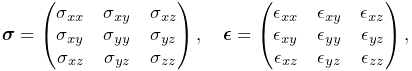$\boldsymbol{\sigma}=\left(\begin{matrix}\sigma_{xx}&\sigma_{xy}&\sigma_{xz}\\ \sigma_{xy}&\sigma_{yy}&\sigma_{yz}\\ \sigma_{xz}&\sigma_{yz}&\sigma_{zz}\end{matrix}\right),\quad\boldsymbol{% \epsilon}=\left(\begin{matrix}\epsilon_{xx}&\epsilon_{xy}&\epsilon_{xz}\\ \epsilon_{xy}&\epsilon_{yy}&\epsilon_{yz}\\ \epsilon_{xz}&\epsilon_{yz}&\epsilon_{zz}\end{matrix}\right),$

(6.8)

and can be expressed as 6-vectors using Voigt notation:

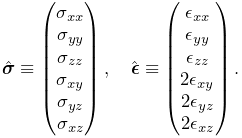$\hat{\boldsymbol{\sigma}}\equiv\left(\begin{matrix}\sigma_{xx}\\ \sigma_{yy}\\ \sigma_{zz}\\ \sigma_{xy}\\ \sigma_{yz}\\ \sigma_{xz}\end{matrix}\right),\quad\hat{\boldsymbol{\epsilon}}\equiv\left(% \begin{matrix}\epsilon_{xx}\\ \epsilon_{yy}\\ \epsilon_{zz}\\ 2\epsilon_{xy}\\ 2\epsilon_{yz}\\ 2\epsilon_{xz}\end{matrix}\right).$

(6.9)

This allows the constitutive mapping to be expressed in matrix form as

$\hat{\boldsymbol{\sigma}}={\bf D}\,\hat{\boldsymbol{\epsilon}},$

(6.10)

where ${\bf D}$ is the $6\times 6$ elasticity matrix.

Different Voigt notation mappings appear in the literature with regard to off-diagonal matrix entries. We use the one employed by FEBio [13]. Another common mapping is

$\hat{\boldsymbol{\sigma}}\equiv\left(\begin{matrix}\sigma_{xx}&\sigma_{yy}&% \sigma_{zz}&\sigma_{yz}&\sigma_{xz}&\sigma_{xy}\end{matrix}\right)^{T}.$

Traditionally, Cauchy strain is computed from the symmetric part of the deformation gradient ${\bf F}$ using the formula

$\boldsymbol{\epsilon}=\frac{{\bf F}^{T}+{\bf F}}{2}-{\bf I},$

(6.11)

where ${\bf I}$ is the $3\times 3$ identity matrix. However, ArtiSynth materials support corotation, in which rotations are first removed from ${\bf F}$ using a polar decomposition

${\bf F}={\bf R}{\bf P},$

(6.12)

where ${\bf R}$ is a (right-handed) rotation matrix and ${\bf P}$ is symmetric matrix. ${\bf P}$ is then used to compute the Cauchy strain:

$\boldsymbol{\epsilon}={\bf P}-{\bf I}.$

(6.13)

Corotation is the default behavior for linear materials in ArtiSynth and allows models to handle large scale rotational deformations [18, 16].

For linear materials, the stress/strain response is computed at a single integration point in the center of each element. This is done to improve computational efficiency, as it allows the precomputation of stiffness matrices that map nodal displacements onto nodal forces for each element. This precomputed matrix can then be adjusted during each simulation step to account for the rotation ${\bf R}$ computed at each element’s integration point [18, 16].

Specific linear material types are listed in the subsections below. All are subclasses of LinearMaterialBase, and in addition to their individual properties, all export a corotation property (default value true) that controls whether corotation is applied.

6.10.1.1 LinearMaterial

LinearMaterial is a standard isotropic linear material, which is also the default material for FEM models. Its elasticity matrix is given by

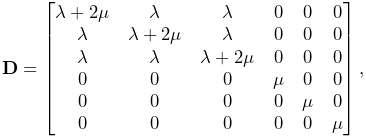${\bf D}=\begin{bmatrix}\lambda+2\mu&\lambda&\lambda&0&0&0\\ \lambda&\lambda+2\mu&\lambda&0&0&0\\ \lambda&\lambda&\lambda+2\mu&0&0&0\\ 0&0&0&\mu&0&0\\ 0&0&0&0&\mu&0\\ 0&0&0&0&0&\mu\end{bmatrix},$

(6.14)

where the Lamé parameters $\lambda$ and $\mu$ are derived from Young’s modulus and Poisson’s ratio $\nu$ via

$\lambda=\dfrac{E\nu}{(1+\nu)(1-2\nu)},\quad\mu=\dfrac{E}{2(1+\nu)}.$

(6.15)

The material behavior is controlled by the following properties:

	Property	Description	Default	Field
	YoungsModulus	Young’s modulus	500000	✓
$\nu$	PoissonsRatio	Poisson’s ratio	0.33
	corotated	applies corotation if true	true

LinearMaterials can be created with the following constructors:

LinearMaterial()	Create with default properties.
LinearMaterial (double E, double nu)	Create with specified and $\nu$ .
LinearMaterial (double E, double nu, boolean corotated)	Create with specified , $\nu$ and corotation.

6.10.1.2 TransverseLinearMaterial

TransverseLinearMaterial is a transversely isotropic linear material whose behavior is symmetric about a prescribed polar axis. If the polar axis is parallel to the axis, then the elasticity matrix is specified most easily in terms of its inverse, or compliance matrix, according to

${\bf D}^{-1}=\begin{bmatrix}\dfrac{1}{E_{xy}}&-\dfrac{\nu_{yx}}{E_{xy}}&-% \dfrac{\nu_{z}}{E_{z}}&0&0&0\\ -\dfrac{\nu_{yx}}{E_{xy}}&\dfrac{1}{E_{xy}}&-\dfrac{\nu_{z}}{E_{z}}&0&0&0\\ -\dfrac{\nu_{z}}{E_{z}}&-\dfrac{\nu_{z}}{E_{z}}&\dfrac{1}{E_{z}}&0&0&0\\ 0&0&0&\dfrac{2(1+\nu_{yx})}{E_{xy}}&0&0\\ 0&0&0&0&\dfrac{1}{G}&0\\ 0&0&0&0&0&\dfrac{1}{G}\end{bmatrix},$

where $E_{xy}$ and $E_{z}$ are Young’s moduli transverse and parallel to the axis, respectively, $\nu_{xy}$ and $\nu_{z}$ are Poisson’s ratios transverse and parallel to the axis, and is the shear modulus.

The material behavior is controlled by the following properties:

	Property	Description	Default	Field
$(E_{xy},E_{z})^{T}$	youngsModulus	Young’s moduli transverse and parallel to the axis	$(500000,500000)^{T}$	✓
$(\nu_{xy},\nu_{z})^{T}$	poissonsRatio	Poisson’s ratios transverse and parallel to the axis	$(0.33,0.33)^{T}$
	shearModulus	shear modulus	187970	✓
	direction	direction of the polar axis	$(0,0,1)^{T}$	✓
	corotated	applies corotation if true	true

The youngsModulus and poissonsRatio properties are both described by Vector2d objects, while direction is described by a Vector3d. The direction property (as well as youngsModulus and shearModulus) can be bound to a field to allow its value to vary over an FEM model (Section 7.2).

TransverseLinearMaterials can be created with the following constructors:

TransverseLinearMaterial()	Create with default properties.
TransverseLinearMaterial (Vector2d E, double G, MVector2d nu, boolean corotated)	Create with specified , , $\nu$ and corotation.

6.10.1.3 AnisotropicLinearMaterial

AnisotropicLinearMaterial is a general anisotropic linear material whose behavior is specified by an arbitrary (symmetric) elasticity matrix ${\bf D}$ . The material behavior is controlled by the following properties:

	Property	Description	Default	Field
${\bf D}$	stiffnessTensor	symmetric $6\times 6$ elasticity matrix
	corotated	applies corotation if true	true

The default value for stiffnessTensor is an isotropic elasticity matrix corresponding to and $\nu=0.33$ .

AnisotropicLinearMaterials can be created with the following constructors:

AnisotropicLinearMaterial()	Create with default properties.
AnisotropicLinearMaterial (Matrix6dBase D)	Create with specified elasticity ${\bf D}$ .
AnisotropicLinearMaterial (Matrix6dBase D, boolean corotated)	Create with specified ${\bf D}$ and corotation.

6.10.2 Hyperelastic materials

A hyperelastic material is defined by a strain energy density function that is in general a function of the deformation gradient ${\bf F}$ , and more specifically a quantity derived from ${\bf F}$ that is rotationally invariant, such as the right Cauchy Green tensor ${\bf C}\equiv{\bf F}^{T}{\bf F}$ , the left Cauchy Green tensor ${\bf B}\equiv{\bf F}{\bf F}^{T}$ , or Green strain

${\bf E}=\frac{1}{2}\left({\bf F}^{T}{\bf F}-{\bf I}\right).$

(6.15)

is often described with respect to the first or second invariants of these quantities, denoted by $I_{1}$ and $I_{2}$ and defined with respect to a given matrix ${\bf A}$ by

$I_{1}\equiv\operatorname{tr}({\bf A}),\quad I_{2}\equiv\frac{1}{2}\left(% \operatorname{tr}({\bf A})^{2}-\operatorname{tr}({\bf A}^{2})\right).$

(6.16)

Alternatively, is sometimes defined with respect to the three principal stretches of the deformation, $\lambda_{i},i\in{1,2,3}$ , which are the eigenvalues of the symmetric component ${\bf P}$ of the polar decomposition of ${\bf F}$ in (6.12).

If is expressed with respect to ${\bf E}$ , then the second Piola-Kirchhoff stress ${\bf S}$ is given by

${\bf S}=\frac{\partial W}{\partial{\bf E}}$

(6.17)

from which the Cauchy stress can be obtained via

$\boldsymbol{\sigma}=\frac{1}{J}{\bf F}{\bf S}{\bf F}^{T},\quad J\equiv\det{\bf F}.$

(6.18)

Many of the hyperelastic materials described below are incompressible, in the sense that is partitioned into a deviatoric component that is volume invariant and a dilational component that depends solely on volume changes. Volume change is characterized by $J=\det{\bf F}$ , with the change in volume given by $dV=J^{1/3}$ and indicating no volume change. Deviatoric changes are characterized by $\bar{\bf F}$ , with

$\bar{\bf F}=J^{-1/3}{\bf F},$

(6.19)

and so the partitioned strain energy density function assumes the form

$W({\bf F})=\bar{W}(\bar{\bf F})+U(J),$

(6.20)

where the $\bar{W}()$ term is the deviatoric contribution and is the volumetric potential that enforces incompressibility. $\bar{W}()$ may also be expressed with respect to the right deviatoric Cauchy Green tensor $\bar{\bf C}$ or the left deviatoric Cauchy Green tensor $\bar{\bf B}$ , respectively defined by

$\bar{\bf C}=J^{-2/3}{\bf C},\quad\bar{\bf B}=J^{-2/3}{\bf B}.$

(6.21)

ArtiSynth supplies different forms of , as specified by a material’s bulkPotential property and detailed in Section 6.7.3. All of the available potentials depend on a bulkModulus property $\kappa$ , and so is often expressed as $U(\kappa,J)$ . A larger bulk modulus will make the material more incompressible, with effective incompressibility typically achieved by setting $\kappa$ to a value that exceeds the other elastic moduli in the material by a factor of 100 or more. All incompressible materials are subclasses of IncompressibleMaterialBase.

6.10.2.1 St Venant-Kirchoff material

StVenantKirchoffMaterial is a compressible isotropic material that extends isotropic linear elasticity to large deformations. The strain energy density is most easily expressed as a function of the Green strain ${\bf E}$ :

$W({\bf E})=\frac{\lambda}{2}\operatorname{tr}({\bf E})^{2}+\mu\operatorname{tr% }({\bf E}^{2}),$

(6.22)

where the Lamé parameters $\lambda$ and $\mu$ are derived from Young’s modulus and Poisson’s ratio $\nu$ according to (6.15). From this definition it follows that the second Piola-Kirchoff stress tensor is given by

${\bf S}=\lambda\operatorname{tr}({\bf E}){\bf I}+2\mu{\bf E}.$

(6.23)

The material behavior is controlled by the following properties:

	Property	Description	Default	Field
	YoungsModulus	Young’s modulus	500000	✓
$\nu$	PoissonsRatio	Poisson’s ratio	0.33

StVenantKirchoffMaterials can be created with the following constructors:

StVenantKirchoffMaterial()	Create with default properties.
StVenantKirchoffMaterial (double E, double nu)	Create with specified elasticity and $\nu$ .

6.10.2.2 Neo-Hookean material

NeoHookeanMaterial is a compressible isotropic material with a strain energy density expressed as a function of the first invariant $I_{1}$ of the right Cauchy-Green tensor ${\bf C}$ and $J=\det{\bf F}$ :

$W({\bf C},J)=\frac{\mu}{2}\left(I_{1}-3\right)-\mu\ln(J)+\frac{\lambda}{2}\ln(% J)^{2},$

(6.23)

where the Lamé parameters $\lambda$ and $\mu$ are derived from Young’s modulus and Poisson’s ratio $\nu$ via (6.15). The Cauchy stress can be expressed in terms of the left Cauchy-Green tensor ${\bf B}$ as

$\boldsymbol{\sigma}=\frac{\mu}{J}{\bf B}+\frac{\lambda\ln(J)-\mu}{J}{\bf I}.$

(6.24)

The material behavior is controlled by the following properties:

	Property	Description	Default	Field
	YoungsModulus	Young’s modulus	500000	✓
$\nu$	PoissonsRatio	Poisson’s ratio	0.33

NeoHookeanMaterials can be created with the following constructors:

NeoHookeanMaterial()	Create with default properties.
NeoHookeanMaterial (double E, double nu)	Create with specified elasticity and $\nu$ .

6.10.2.3 Incompressible neo-Hookean material

IncompNeoHookeanMaterial is an incompressible version of the neo-Hookean material, with a strain energy density expressed in terms of the first invariant $\bar{I}_{1}$ of the deviatoric right Cauchy-Green tensor $\bar{\bf C}$ , plus a potential function $U(\kappa,J)$ to enforce incompressibility:

$W(\bar{\bf C},J)=\frac{G}{2}\left(\bar{I}_{1}-3\right)+U(\kappa,J).$

(6.24)

The material behavior is controlled by the following properties:

	Property	Description	Default	Field
	shearModulus	shear modulus	150000	✓
$\kappa$	bulkModulus	bulk modulus for incompressibility	100000	✓
	bulkPotential	incompressibility potential function $U(\kappa,J)$	QUADRATIC

IncompNeoHookeanMaterials can be created with the following constructors:

IncompNeoHookeanMaterial()	Create with default properties.
IncompNeoHookeanMaterial (double G, double kappa)	Create with specified elasticity and $\kappa$ .

6.10.2.4 Mooney-Rivlin material

MooneyRivlinMaterial is an incompressible isotropic material with a strain energy density expressed as a polynomial of the first and second invariants $\bar{I}_{1}$ and $\bar{I}_{2}$ of the right deviatoric Cauchy-Green tensor $\bar{\bf C}$ . ArtiSynth supplies a five parameter version of this model, with a strain energy density given by

$W(\bar{\bf C},J)=C_{10}(\bar{I}_{1}-3)+C_{01}(\bar{I}_{2}-3)+C_{11}(\bar{I}_{1% }-3)(\bar{I}_{2}-3)+C_{20}(\bar{I}_{1}-3)^{2}+C_{02}(\bar{I}_{2}-3)^{2}+U(% \kappa,J).$

(6.24)

A two-parameter version ( $C_{1}$ , $C_{2}$ ) is often found in the literature, consisting of only the first two terms:

$W(\bar{\bf C},J)=C_{1}(\bar{I}_{1}-3)+C_{2}(\bar{I}_{2}-3)+U(\kappa,J),\qquad C% _{1}\equiv C_{10},\quad C_{2}\equiv C_{01}.$

(6.25)

The material behavior is controlled by the following properties:

	Property	Description	Default	Field
$C_{10}$	C10	first coefficient	150000	✓
$C_{01}$	C01	second coefficient	0	✓
$C_{11}$	C11	third coefficient	0	✓
$C_{20}$	C20	fourth coefficient	0	✓
$C_{02}$	C02	fifth coefficient	0	✓
$\kappa$	bulkModulus	bulk modulus for incompressibility	100000	✓
	bulkPotential	incompressibility potential function $U(\kappa,J)$	QUADRATIC

MooneyRivlinMaterials can be created with the following constructors:

MooneyRivlinMaterial()	Create with default properties.
MooneyRivlinMaterial (double C10, double C01, double C11, Mdouble C20, double C02, double kappa)	Create with specified coefficients.

6.10.2.5 Ogden material

OgdenMaterial is an incompressible material with a strain energy density expressed as a function of the deviatoric principal stretches $\bar{\lambda}_{i},i\in{1,2,3}$ :

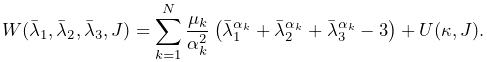$W(\bar{\lambda}_{1},\bar{\lambda}_{2},\bar{\lambda}_{3},J)=\sum_{k=1}^{N}\frac% {\mu_{k}}{\alpha_{k}^{2}}\left(\bar{\lambda}_{1}^{\alpha_{k}}+\bar{\lambda}_{2% }^{\alpha_{k}}+\bar{\lambda}_{3}^{\alpha_{k}}-3\right)+U(\kappa,J).$

(6.25)

ArtiSynth allows a maximum of six terms, corresponding to , and the material behavior is controlled by the following properties:

	Property	Description	Default	Field
$\mu_{1}$	Mu1	first multiplier	300000	✓
$\mu_{2}$	Mu2	second multiplier	0	✓
...	...	...	0	✓
$\mu_{6}$	Mu6	final multiplier	0	✓
$\alpha_{1}$	Alpha1	first multiplier	2	✓
$\alpha_{2}$	Alpha2	second multiplier	2	✓
...	...	...	2	✓
$\alpha_{6}$	Alpha6	final multiplier	2	✓
$\kappa$	bulkModulus	bulk modulus for incompressibility	100000	✓
	bulkPotential	incompressibility potential function $U(\kappa,J)$	QUADRATIC

OgdenMaterials can be created with the following constructors:

OgdenMaterial()	Create with default properties.
OgdenMaterial (double[] mu, double[] alpha, double kappa)	Create with specified $\mu$ , $\alpha$ and $\kappa$ values.

6.10.2.6 Fung orthotropic material

FungOrthotropicMaterial is an incompressible orthotropic material defined with respect to an -- coordinate system expressed by a $3\times 3$ rotation matrix ${\bf R}$ . The strain energy density is expressed as a function of the deviatoric Green strain

$\bar{\bf E}\equiv\frac{1}{2}\left(\bar{\bf C}-{\bf I}\right)$

(6.25)

and the three unit direction vectors ${\bf a}_{1},\,{\bf a}_{2},\,{\bf a}_{3}$ representing the columns of ${\bf R}$ . Letting ${\bf A}_{i}\equiv{\bf a}_{i}{\bf a}_{i}^{T}$ and defining

$\alpha_{i}\equiv{\bf A}_{i}:\bar{\bf E}=\operatorname{tr}({\bf a}_{i}^{T}\bar{% \bf E}\,{\bf a}_{i}),\quad\beta_{i}\equiv{\bf A}_{i}:\bar{\bf E}^{2}=% \operatorname{tr}({\bf a}_{i}^{T}\bar{\bf E}^{2}\,{\bf a}_{i}),\quad$

(6.26)

the energy density is given by

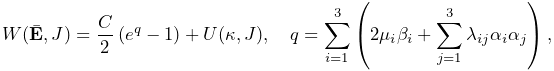$W(\bar{\bf E},J)=\frac{C}{2}\left(e^{q}-1\right)+U(\kappa,J),\quad q=\sum_{i=1% }^{3}\left(2\mu_{i}\beta_{i}+\sum_{j=1}^{3}\lambda_{ij}\alpha_{i}\alpha_{j}% \right),$

(6.27)

where is a material coefficient and $\mu_{i}$ and $\lambda_{ij}$ are the orthotropic Lamé parameters.

At present, the coordinate frame ${\bf R}$ is not defined in the material, but can be specified on a per-element basis using the element method setFrame(Matrix3dBase). For example:

⬇

RotationMatrix3d R;

FemModel3d fem;

...

for (FemElement3d elem : fem.getElements()) {

... computer R as required for the element ...

elem.setFrame (R);

}

One should be careful to ensure that the argument to setFrame() is in fact an orthogonal rotation matrix as this will not be otherwise enforced.

The material behavior is controlled by the following properties:

	Property	Description	Default	Field
$\mu_{1}$	mu1	second Lamé parameter along	1000	✓
$\mu_{2}$	mu2	second Lamé parameter along	1000	✓
$\mu_{3}$	mu3	second Lamé parameter along	1000	✓
$\lambda_{11}$	lam11	first Lamé parameter along	2000	✓
$\lambda_{22}$	lam22	first Lamé parameter along	2000	✓
$\lambda_{33}$	lam33	first Lamé parameter along	2000	✓
$\lambda_{12}$	lam12	first Lamé parameter for	2000	✓
$\lambda_{23}$	lam23	first Lamé parameter for	2000	✓
$\lambda_{31}$	lam31	first Lamé parameter for	2000	✓
	C	C coefficient	1500	✓
$\kappa$	bulkModulus	bulk modulus for incompressibility	100000	✓
	bulkPotential	incompressibility potential function $U(\kappa,J)$	QUADRATIC

FungOrthotropicMaterials can be created with the following constructors:

FungOrthotropicMaterial()	Create with default properties.
FungOrthotropicMaterial (double mu1, double mu2, double mu3, Mdouble lam11, double lam22, double lam33, double lam12, Mdouble lam23, double lam31, double C, double kappa)	Create with specified properties.

6.10.2.7 Yeoh material

YeohMaterial is an incompressible isotropic material that implements a Yeoh model with a strain energy density containing up to five terms:

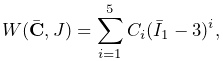$W(\bar{\bf C},J)=\sum_{i=1}^{5}C_{i}(\bar{I}_{1}-3)^{i},$

(6.27)

where $\bar{I}_{1}$ is the first invariant of the right deviatoric Cauchy Green tensor and $C_{i}$ are the material coefficients. The material behavior is controlled by the following properties:

	Property	Description	Default	Field
$C_{1}$	C1	first coefficient (shear modulus)	150000	✓
$C_{2}$	C2	second coefficient	0	✓
$C_{3}$	C3	third coefficient	0	✓
$C_{4}$	C4	fourth coefficient	0	✓
$C_{5}$	C5	fifth coefficient	0	✓
$\kappa$	bulkModulus	bulk modulus for incompressibility	100000	✓
	bulkPotential	incompressibility potential function $U(\kappa,J)$	QUADRATIC

YeohMaterials can be created with the following constructors:

YeohMaterial()	Create with default properties.
YeohMaterial (double C1, double C2, double C3, double kappa)	Create three term material with $C_{1}$ , $C_{2}$ , $C_{3}$ , $\kappa$ .
YeohMaterial (double C1, double C2, double C3, double C4, Mdouble C5, double kappa)	Create five term material with $C_{1}$ , ..., $C_{5}$ , $\kappa$ .

6.10.2.8 Arruda-Boyce material

ArrudaBoyceMaterial is an incompressible isotropic material that implements the Arruda-Boyce model [2]. Its strain energy density is given by

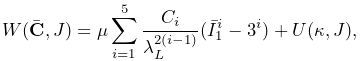$W(\bar{\bf C},J)=\mu\sum_{i=1}^{5}\frac{C_{i}}{\lambda_{L}^{2(i-1)}}(\bar{I}_{% 1}^{i}-3^{i})+U(\kappa,J),$

(6.27)

where $\mu$ is the initial modulus, $\lambda_{L}$ the locking stretch, $\bar{I}_{1}$ the first invariant of the right deviatoric Cauchy Green tensor, and

$C=\left\{\frac{1}{2},\;\frac{1}{20},\;\frac{11}{1050},\;\frac{19}{7000},\;% \frac{519}{673750}\right\}.$

The material behavior is controlled by the following properties:

	Property	Description	Default	Field
$\mu$	mu	initial modulus	1000	✓
$\lambda_{L}$	lambdaMax	locking stretch	2.0	✓
$\kappa$	bulkModulus	bulk modulus for incompressibility	100000	✓
	bulkPotential	incompressibility potential function $U(\kappa,J)$	QUADRATIC

ArrudaBoyceMaterials can be created with the following constructors:

ArrudaBoyceMaterial()	Create with default properties.
ArrudaBoyceMaterial (double mu, double lmax, double kappa)	Create with specified $\mu$ , $\lambda_{L}$ , $\kappa$ .

6.10.2.9 Veronda-Westmann material

VerondaWestmannMaterial is an incompressible isotropic material that implements the Veronda-Westmann model [27]. Its strain energy density is given by

${\bf W}(\bar{\bf C},J)=C_{1}\left(e^{C_{2}(\bar{I}_{1}-3)}-1\right)-\frac{C_{1% }C_{2}}{2}(\bar{I}_{2}-3)+U(\kappa,J),$

(6.28)

where $C_{1}$ and $C_{2}$ are material coefficients and $\bar{I}_{1}$ and $\bar{I}_{2}$ the first and second invariants of the right deviatoric Cauchy Green tensor.

The material behavior is controlled by the following properties:

	Property	Description	Default	Field
$C_{1}$	C1	first coefficient	1000	✓
$C_{2}$	C2	second coefficient	10	✓
$\kappa$	bulkModulus	bulk modulus for incompressibility	100000	✓
	bulkPotential	incompressibility potential function $U(\kappa,J)$	QUADRATIC

VerondaWestmannMaterials can be created with the following constructors:

VerondaWestmannMaterial()	Create with default properties.
VerondaWestmannMaterial (double C1, double C2, double kappa)	Create with specified ${\bf C}_{1}$ , $C_{2}$ , and $\kappa$ .

6.10.2.10 Incompressible material

IncompressibleMaterial is an incompressible isotropic material that implements pure incompressibility, with an energy density function given by

$W(J)=U(\kappa,J).$

(6.28)

Because it responds only to dilational strains, it must be used in conjunction with another material to resist deviatoric strains. In this context, it can be used to provide dilational support to deviatoric-only materials such as the FullBlemkerMuscle (Section 6.10.3.3).

The material behavior is controlled by the following properties:

	Property	Description	Default	Field
$\kappa$	bulkModulus	bulk modulus for incompressibility	100000	✓
	bulkPotential	incompressibility potential function $U(\kappa,J)$	QUADRATIC

IncompressibleMaterials can be created with the following constructors:

IncompressibleMaterial()	Create with default values.
IncompressibleMaterial (double kappa)	Create with specified $\kappa$ .

6.10.3 Muscle materials

Muscle materials are used to exert stress along a particular direction within a material. This stress may contain both an active component, which depends on the muscle excitation, and a passive component, which depends solely on the stretch along the prescribed direction. Because most muscle materials act only along one direction, they are typically deployed within an FEM as additional materials that act in addition to an underlying material. This can be done using either muscle bundles within a FemMuscleModel (Section 6.9.1.1) or material bundles within any FEM model (Sections 6.8 and 7.5.2).

All of the muscle materials described below assume (near) incompressibility, and so the directional stress is a function of the deviatoric stretch $\bar{\lambda}$ along the muscle direction instead of the overall stretch $\lambda$ . The former can be determined from the latter via

$\bar{\lambda}=\lambda J^{-1/3},$

(6.28)

where is the determinant of the deformation gradient. The directional Cauchy stress $\boldsymbol{\sigma}_{d}$ resulting from the material is computed from

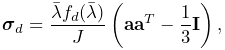$\boldsymbol{\sigma}_{d}=\frac{\bar{\lambda}f_{d}(\bar{\lambda})}{J}\left({\bf a% }{\bf a}^{T}-\frac{1}{3}{\bf I}\right),$

(6.29)

where $f_{d}(\bar{\lambda})$ is a force term, ${\bf a}$ is a unit vector indicating the current muscle direction in spatial coordinates, and ${\bf I}$ is the $3\times 3$ identity matrix. In a purely passive case when the force arises from a stress energy density function $W(\bar{\lambda})$ , we have

$f_{d}(\bar{\lambda})=\frac{\partial W(\bar{\lambda})}{\partial\bar{\lambda}}.$

(6.30)

The muscle direction is specified in one of two ways, depending on how the muscle material is deployed. All muscle materials export a property restDir which specifies the direction in material (rest) coordinates. It has a default value of $(1,0,0)^{T}$ , and can be either set explicitly or bound to a field to allow it to vary over the entire model (Section 7.5.2). However, if a muscle material is deployed within a muscle bundle (Section 6.9.1), then the restDir property is ignored and the direction is instead specified by the MuscleElementDesc components contained within the bundle (Section 6.9.3).

Likewise, muscle excitation is specified using the material’s excitation property, unless the material is deployed within a muscle bundle, in which case it is controlled by the excitation property of the bundle.

6.10.3.1 Generic muscle

GenericMuscle is a muscle material whose force term $f_{d}(\bar{\lambda})$ is given by

$f_{d}(\bar{\lambda})=a\sigma_{max}+f_{p}(\bar{\lambda}),$

(6.31)

where is the excitation signal, $\sigma_{max}$ is a maximum stress term, and $f_{p}(\bar{\lambda})$ is a passive force given by

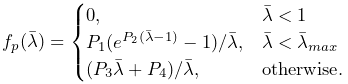$f_{p}(\bar{\lambda})=\begin{cases}0,&\bar{\lambda}<1\\ P_{1}(e^{P_{2}(\bar{\lambda}-1)}-1)/\bar{\lambda},&\bar{\lambda}<\bar{\lambda}% _{max}\\ (P_{3}\bar{\lambda}+P_{4})/\bar{\lambda},&\mathrm{otherwise}.\end{cases}$

(6.32)

In the equation above, $P_{1}$ is the exponential stress coefficient, $P_{2}$ is the uncrimping factor, and $P_{3}$ and $P_{4}$ are computed to provide continuity at $\bar{\lambda}=\bar{\lambda}_{max}$ .

The material behavior is controlled by the following properties:

	Property	Description	Default	Field
$\sigma_{max}$	maxStress	maximum stress	30000	✓
$\bar{\lambda}_{max}$	maxLambda	$\bar{\lambda}$ at upper limit of exponential section of $f_{p}(\bar{\lambda})$	1.4	✓
$P_{1}$	expStressCoeff	exponential stress coefficient	0.05	✓
$P_{2}$	uncrimpingFactor	uncrimping factor	6.6	✓
${\bf a}_{0}$	restDir	direction in material coordinates	$(1,0,0)^{T}$	✓
	excitation	activation signal	0

GenericMuscles can be created with the following constructors:

GenericMuscle()	Create with default values.
GenericMuscle (double maxLambda, double maxStress, Mdouble expStressCoef, double uncrimpFactor)	Create with specified $\bar{\lambda}_{max}$ , $\sigma_{max}$ , $P_{1}$ , $P_{2}$ .

The constructors do not specify restDir. If the material is not being deployed within a muscle bundle, then restDir should also be set appropriately, either directly or via a field (Section 7.5.2).

6.10.3.2 Blemker muscle

BlemkerMuscle is a muscle material implementing the directional component of the model proposed by Sylvia Blemker [5]. Its force term $f_{d}(\bar{\lambda})$ is given by

$f_{d}(\bar{\lambda})=\sigma_{max}(af_{a}(\bar{\lambda})+f_{p}(\bar{\lambda}))/% \bar{\lambda}_{opt},$

(6.32)

where $\sigma_{max}$ is a maximum stress term, is the excitation signal, $f_{a}(\bar{\lambda})$ is an active force-length curve, and $f_{p}(\bar{\lambda})$ is the passive force. $f_{a}(\bar{\lambda})$ and $f_{p}(\bar{\lambda})$ are described in terms of $\hat{\lambda}\equiv\bar{\lambda}/\bar{\lambda}_{opt}$ :

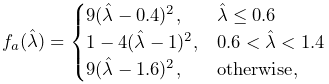$f_{a}(\hat{\lambda})=\begin{cases}9(\hat{\lambda}-0.4)^{2},&\hat{\lambda}\leq 0% .6\\ 1-4(\hat{\lambda}-1)^{2},&0.6<\hat{\lambda}<1.4\\ 9(\hat{\lambda}-1.6)^{2},&\mathrm{otherwise},\end{cases}$

(6.33)

and

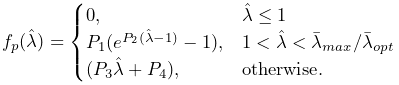$f_{p}(\hat{\lambda})=\begin{cases}0,&\hat{\lambda}\leq 1\\ P_{1}(e^{P_{2}(\hat{\lambda}-1)}-1),&1<\hat{\lambda}<\bar{\lambda}_{max}/\bar{% \lambda}_{opt}\\ (P_{3}\hat{\lambda}+P_{4}),&\mathrm{otherwise}.\end{cases}$

(6.34)

In the equation for $f_{p}(\bar{\lambda})$ , $P_{1}$ is the exponential stress coefficient, $P_{2}$ is the uncrimping factor, and $P_{3}$ and $P_{4}$ are computed to provide continuity at $\hat{\lambda}=\bar{\lambda}_{max}/\bar{\lambda}_{opt}$ .

The material behavior is controlled by the following properties:

	Property	Description	Default	Field
$\sigma_{max}$	maxStress	maximum stress	300000	✓
$\bar{\lambda}_{opt}$	optLambda	$\bar{\lambda}$ at peak of $f_{a}(\bar{\lambda})$	1	✓
$\bar{\lambda}_{max}$	maxLambda	$\bar{\lambda}$ at upper limit of exponential section of $f_{p}(\bar{\lambda})$	1.4	✓
$P_{1}$	expStressCoeff	exponential stress coefficient	0.05	✓
$P_{2}$	uncrimpingFactor	uncrimping factor	6.6	✓
${\bf a}_{0}$	restDir	direction in material coordinates	$(1,0,0)^{T}$	✓
	excitation	activation signal	0

BlemkerMuscles can be created with the following constructors:

BlemkerMuscle()	Create with default values.
BlemkerMuscle (double maxLam, double optLam, Mdouble maxStress, double expStressCoef, double uncrimpFactor)	Create with specified $\bar{\lambda}_{max}$ , $\bar{\lambda}_{opt}$ , $\sigma_{max}$ , $P_{1}$ , $P_{2}$ .

The constructors do not specify restDir. If the material is not being deployed within a muscle bundle, then restDir should also be set appropriately, either directly or via a field (Section 7.5.2).

6.10.3.3 Full Blemker muscle

FullBlemkerMuscle is a muscle material implementing the entire model proposed by Sylvia Blemker [5]. This includes the directional stress described in Section 6.10.3.2, plus additional passive terms to model the tissue material matrix. The latter is based on a strain energy density function $W_{m}$ given by

$W_{m}(\bar{\bf B},\lambda)=G_{1}\bar{B}_{1}^{2}+G_{2}\bar{B}_{2}^{2}$

(6.34)

where $G_{1}$ and $G_{2}$ are the along-fibre and cross-fibre shear moduli, respectively, and $\bar{B}_{1}$ and $\bar{B}_{2}$ are Criscione invariants. The latter are defined as follows: Let $\bar{I}_{1}$ and $\bar{I}_{2}$ be the invariants of the deviatoric left Cauchy Green tensor $\bar{\bf B}$ , ${\bf a}$ the unit vector giving the current muscle direction in spatial coordinates, and $\bar{I}_{4}$ and $\bar{I}_{5}$ additional invariants defined by

$\bar{I}_{4}\equiv\bar{\lambda}^{2},\quad\bar{I}_{5}\equiv\bar{I}_{4}\,{\bf a}^% {T}\bar{\bf B}{\bf a}.$

(6.35)

Then, defining

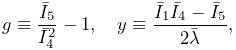$g\equiv\frac{\bar{I}_{5}}{\bar{I}_{4}^{2}}-1,\quad y\equiv\frac{\bar{I}_{1}% \bar{I}_{4}-\bar{I}_{5}}{2\bar{\lambda}},$

$\bar{B}_{1}$ and $\bar{B}_{2}$ are given by

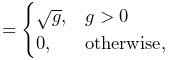	$\displaystyle\bar{B}_{1}$	$\displaystyle=\begin{cases}\sqrt{g},&g>0\\ 0,&\mathrm{otherwise},\\ \end{cases}$		(6.36)
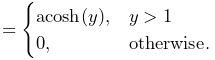	$\displaystyle\bar{B}_{2}$	$\displaystyle=\begin{cases}\mathrm{acosh}(y),&y>1\\ 0,&\mathrm{otherwise}.\\ \end{cases}$		(6.37)

At present, FullBlemkerMuscle does not implement a volumetric potential function . That means it responds solely to deviatoric strains, and so if it is being used as a model’s primary material, it should be augmented with an additional material to provide resistance to compression. A simple choice for this is the purely incompressible material IncompressibleMaterial, described in Section 6.10.2.10.

The material behavior is controlled by the following properties:

	Property	Description	Default	Field
$\sigma_{max}$	maxStress	maximum stress	300000	✓
$\bar{\lambda}_{opt}$	optLambda	$\bar{\lambda}$ at peak of $f_{a}(\bar{\lambda})$	1	✓
$\bar{\lambda}_{max}$	maxLambda	$\bar{\lambda}$ at upper limit of exponential section of $f_{p}(\bar{\lambda})$	1.4	✓
$P_{1}$	expStressCoeff	exponential stress coefficient	0.05	✓
$P_{2}$	uncrimpingFactor	uncrimping factor	6.6	✓
$G_{1}$	G1	along-fibre shear modulus	0	✓
$G_{2}$	G2	cross-fibre shear modulus	0	✓
${\bf a}_{0}$	restDir	direction in material coordinates	$(1,0,0)^{T}$	✓
	excitation	activation signal	0

FullBlemkerMuscles can be created with the following constructors:

FullBlemkerMuscle()	Create with default values.
BlemkerMuscle (double maxLam, double optLam, Mdouble maxStress, double expStressCoef, Mdouble uncrimpFactor, double G1, double G2)	Create with $\bar{\lambda}_{max}$ , $\bar{\lambda}_{opt}$ , $\sigma_{max}$ , $P_{1}$ , $P_{2}$ , $G_{1}$ , $G_{2}$ .

The constructors do not specify restDir. If the material is not being deployed within a muscle bundle, then restDir should also be set appropriately, either directly or via a field (Section 7.5.2).

6.10.3.4 Simple force muscle

SimpleForceMuscle is a very simple muscle material whose force term $f_{d}(\bar{\lambda})$ is given by

$f_{d}(\bar{\lambda})=a\sigma_{max},$

(6.38)

where is the excitation signal and $\sigma_{max}$ is a maximum stress term. It can be useful as a debugging tool.

The material behavior is controlled by the following properties:

	Property	Description	Default	Field
$\sigma_{max}$	maxStress	maximum stress	30000	✓
${\bf a}_{0}$	restDir	direction in material coordinates	$(1,0,0)^{T}$	✓
	excitation	activation signal	0

SimpleForceMuscles can be created with the following constructors:

SimpleForceMuscle()	Create with default values.
SimpleForceMuscle (double maxStress)	Create with specified $\sigma_{max}$ .

The constructors do not specify restDir. If the material is not being deployed within a muscle bundle, then restDir should also be set appropriately, either directly or via a field (Section 7.5.2).

6.9 Muscle activated FEM models Bibliography 6.11 Stress, strain and strain energy

Generated on Sun Jan 12 23:00:57 2025 by LaTeXML [LOGO]